Triangles and Pyramids
Playing math!
 I like playing with math. These days, I don’t need that much math for my daily life–enough to calculate whether I’ve got enough gas to get from A to B, to balance my checkbook, to budget for the training class I’m starting, to figure out expenses on Frost and Fire‘s new album… but I don’t need that much math. I was trained as a computer scientist, but it’s been a while since I’ve done O() analysis on an algorithm or used vector math to build a graphics system.
I like playing with math. These days, I don’t need that much math for my daily life–enough to calculate whether I’ve got enough gas to get from A to B, to balance my checkbook, to budget for the training class I’m starting, to figure out expenses on Frost and Fire‘s new album… but I don’t need that much math. I was trained as a computer scientist, but it’s been a while since I’ve done O() analysis on an algorithm or used vector math to build a graphics system.
Math isn’t something I mostly need right now. It’s something I like.
I like thinking about things mathematically, looking for patterns, seeing what I notice, wondering what could explain it. That’s fun stuff.
This evening, I came up with a problem domain for exploring some things about triangles and solids. Jasmine (@jaz_math) and Pete and I spent a couple of hours around the dinner table exploring these questions and bringing various principles from geometry, trigonometry, and calculus to bear on them.
The context
I want to make some little free-standing pyramids that are built with paper. I want to be able to make them by folding a single piece of paper, with only a single piece of tape to hold them together.
Make an isosceles triangle of base b and height l. To start with, I drew one with b = 2 cm and l = 5 cm. Draw it on a sheet of paper, then cut it out. We’ll call this your “source triangle“.

Take a new piece of paper and trace around the source triangle. Then flip the source triangle so it shares one long edge with the previous triangle, and trace it again. Repeat this one more time so you’ve got a drawing with a big shape that sort of curves around a central point, made up of three identical triangles. Cut that shape out. We’ll call this your “net“. Generally, we could call it an n-net where n is the number of triangles it uses.

Fold the net neatly on each of the lines you’ve drawn and then tape the two outside edges together so you’ve got a pyramid that stands on the table. We’ll call this a “pyramid” or a “solid“. If you do it right, it should stand up on its own. You might find it easier to fold the paper over a ruler to get really crisp edges. (Or use the edge of credit card for the full pyramid scheme experience.)
Since it has three sides/triangles, we’ll call it a 3-pyramid or a 3-solid. With more sides, you’d call it an n-solid where n = the number of sides.

To help frame the discussion, here are some diagrams and definitions:
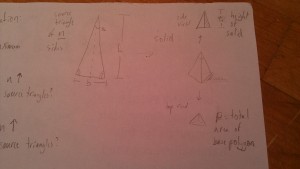
- n = the number of sides in the solid
- b = the base length of the source triangle
- l = the height of the source triangle (perpendicular to base)
- t = the tallness/height of the pyramid after assembly (measured perpendicular to table)
- base polygon = the polygon formed on the table by the edges of the pyramid (visible in top view)
- p = the area of the base polygon
You may find it easier to play with the questions that follow if you make yourself a source triangle, a 3-pyramid, and a 4-pyramid before continuing.
Things to investigate
Maximizing n sides
- What’s the maximum number of sides (n) that you can use to make an n-pyramid out of a single sheet of paper?
- Is your answer true for all source triangles? If yes, why? If not, why?
Playing with height: t
- How does the height of the pyramid change as n increases?
- Does it follow a pattern?
- Is that pattern the same for all source triangles?
- Can you come up with a formula that will accurately predict the height (t) of your n-pyramids?
Playing with area: p
- How does the area of the base polygon change as n increases?
- Does it follow a pattern?
- Is that pattern the same for all source triangles?
- Can you come up with a formula that will accurately predict the base polygon area (p) of your n-pyramids?
- Is there a relationship between the area of the original n-net (the flat sheet of paper) and the area of the base polygon p?
Playing with ratios
- Is there a relationship between t (the pyramid’s height) and p (the base polygon’s area) for a given source triangle? Does it allow you to predict anything as n increases? If so, is it the same for all source triangles?
- We can describe the relationship between a source triangle’s base and height (b and l) as its aspect ratio. What effect does aspect ratio have on the resulting pyramids?
- If you made a series of 3-pyramids where you held the source triangle’s height (l) constant but increased the base (b) by 1 cm for each subsequent triangle, what change would you notice in the height of the resulting 3-pyramids (t)? What kind of relationship is it?
Silhouettes
- If you looked at the pyramid from the side and rotated it so its silhouette was widest, how wide would the silhouette appear at its base? What relationship does the silhouette’s width have with b? Does it depend on n? If so, how?
Onward
We had a lot of fun playing math with these ideas tonight. I hope you have fun too! I’ll post some of the results of our math play later on, but I wanted to let you play with the pyramids on your own first.
These questions are fine for students who’ve had basic geometry, although they’ll have an easier time describing some of the relationships and solving some questions if they’ve had some trigonometry and calculus.
If you have questions, solutions, interesting ideas, things you notice, or things you wonder, please leave a comment!







After further experimentation, I have discovered that the folding process becomes much more challenging at n=10 !